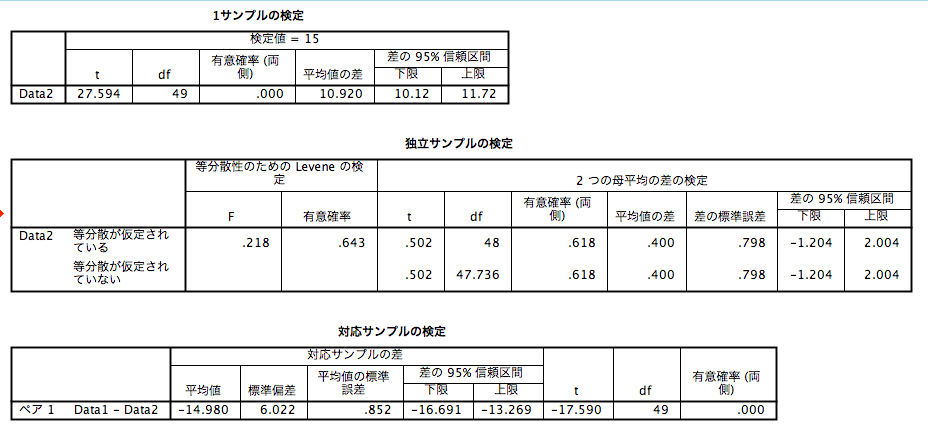
研究分野によって「検定に使用するソフトウェア」のスタンダードは若干異なりますが、SPSSを押さえておけば間違いが無いと思います。そこで、Rの普及を願いSPSSのT検定周りを再現する方法を確認したので紹介します。
検定は実験計画に基づき実施するのが基本と考えます。紹介するデータ例はデタラメです。あくまでSPSSとRの結果が同じになるRのコマンドを紹介します。きちんと実験計画に則り検定を実施していただければと思います。
なお、実行コマンドはR version 4.2.2で確認しています。
実行コマンド
詳細はコメント、パッケージヘルプを確認してください。SPSSのシンタックス出力にdescrパッケージを使用しています。過去に紹介していますので、ぜひ検索してみて下さい。
set.seed(1234)
###R用データ例の作成#####
n <- 50
TestData <- data.frame(Group = sample(paste0("Group", 1:2), n, replace = TRUE),
Effects = sample(c("Low", "Middle", "Hight"), n, replace = TRUE),
Data1 = sample(1:20, n, replace = TRUE),
Data2 = sample(21:30, n, replace = TRUE),
Data3 = sample(1:100, n, replace = TRUE))
########
###SPSS用データ例の作成#####
#作業ディレクトリにTestDataをSPSSで再現するシンタックスとデータファイルが出力されます
#descrパッケージは過去記事を参照ください
#install.packages("descr")
library("descr")
data.frame2txt(TestData, sps.codefile = "TestData.sps",
datafile = "TestData.txt", r.codefile = "TestData.R")
########
###########################################
###1サンプルのT検定で表示される結果の再現##
###########################################
t.test(TestData[, 4], mu = 15)
#One Sample t-test
#data: TestData[, 4]
#t = 27.594, df = 49, p-value < 2.2e-16
#alternative hypothesis: true mean is not equal to 15
###SPSSは差の95%信頼区間であることに注意###
#95 percent confidence interval:
# 25.12475 26.71525
#sample estimates:
# mean of x
# 25.92
###########################################
###独立したT検定で表示される結果の再現#####
###########################################
#等分散性のための Levene の検定
library(car)
levene.test(TestData[, 4], TestData[, 1], center=mean)
#Levene's Test for Homogeneity of Variance (center = mean)
# Df F value Pr(>F)
#group 1 0.2178 0.6428
# 48
#等分散を仮定した場合
t.test(subset(TestData[, 4], TestData[, 1] == "Group1"),
subset(TestData[, 4], TestData[, 1] == "Group2"), var.equal = TRUE)
#Two Sample t-test
#data: subset(TestData[, 4], TestData[, 1] == "Group1") and subset(TestData[, 4], TestData[, 1] == "Group2")
#t = 0.50152, df = 48, p-value = 0.6183
#alternative hypothesis: true difference in means is not equal to 0
#95 percent confidence interval:
# -1.203641 2.003641
#sample estimates:
# mean of x mean of y
# 26.12 25.72
#等分散を仮定しない場合
t.test(subset(TestData[, 4], TestData[, 1] == "Group1"),
subset(TestData[, 4], TestData[, 1] == "Group2"), var.equal = FALSE)
#Welch Two Sample t-test
#data: subset(TestData[, 4], TestData[, 1] == "Group1") and subset(TestData[, 4], TestData[, 1] == "Group2")
#t = 0.50152, df = 47.736, p-value = 0.6183
#alternative hypothesis: true difference in means is not equal to 0
#95 percent confidence interval:
# -1.203871 2.003871
#sample estimates:
# mean of x mean of y
# 26.12 25.72
###########################################
###対応あるT検定で表示される結果の再現#####
###########################################
t.test(TestData[, 3], TestData[, 4], paired = TRUE)
#Paired t-test
#data: TestData[, 3] and TestData[, 4]
#t = -17.59, df = 49, p-value < 2.2e-16
#alternative hypothesis: true difference in means is not equal to 0
#95 percent confidence interval:
# -16.69144 -13.26856
#sample estimates:
#mean of the differences
# -14.98 SPSSによる結果
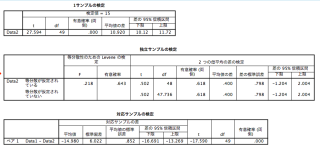
Rの結果と見比べてもらえればと思います。descrパッケージの利用によりSPSSで結果を再現することが可能です。
SPSSのシンタックスは以下の通りです。
/* 1サンプルのT検定
T-TEST
/TESTVAL=15
/MISSING=ANALYSIS
/VARIABLES=Data2
/CRITERIA=CI(.95)./* 独立したサンプルのT検定
T-TEST GROUPS=Group(1 2)
/MISSING=ANALYSIS
/VARIABLES=Data2
/CRITERIA=CI(.95)./*対応あるサンプルのT検定
T-TEST PAIRS=Data1 WITH Data2 (PAIRED)
/CRITERIA=CI(.9500)
/MISSING=ANALYSIS.少しでも、あなたのウェブや実験の解析が楽になりますように!!